프레임워크를 만들며 사용했던 백터의 내적과 외적을 활용을 간단하게 정리해보았다.
1. 시야각 내에 적이 존재하는지 판단하기

빨간 선이 시야 범위,
벡터 A 를 유닛이 정면을 바라보는 벡터,
벡터 B 를 유닛이 적을 바라보는 벡터,
벡터 A와 벡터 B 사이의 사이각을 θ,
벡터 A와 빨간 선 사이의 사이각을 θ'
이라고 정의해 보았다.
시야각 내에 존재하는지 파악하기 위해서는 θ가 θ'보다 작은지를 확인해야 한다. ( θ <= θ' )
arccos을 사용하는 것 보단 cos을 사용하는것이 편하기에 계산의 편의성을 위해 cos을 적용시켜주었다.
cos은 1~0으로 점점 줄어들기에 cosθ >= cosθ' 인지를 확인하면 된다.
우리는 시야각인 θ'의 값을 알고 있기에 θ만 구하면 되는데,
θ의 값을 알기 위해서는 벡터의 내적 공식인
A·B = |A||B|cosθ을
cosθ = (A·B) / (|A|*|B|)로 바꿔주었다.
직관적으로 이해할 수 있도록 A벡터와 B벡터 모두 정규화를 해서 계산해주었다.
정규화한 벡터의 크기는 모두 1이기에, cosθ = A·B가 된다.
정리하자면, A·B >= cosθ' 일 경우, 시야각 내에 적이 존재하는 것이 된다.
다음은 적용한 코드이다.
private List<EnemyUnit> GetAllEnemiesInCone(Vector3 unitPos, Vector3 targetDir, float range, int angle)
{
List<EnemyUnit> enemies = new List<EnemyUnit>();
range *= range;
float cos = Mathf.Cos((angle / 2) * Mathf.Deg2Rad);
cos *= cos;
targetDir.Normalize();
foreach (EnemyUnit enemy in _enemies)
{
if (enemy != null && enemy.isActiveAndEnabled)
{
Vector3 dirVector = enemy.transform.position - unitPos;
float distance = dirVector.sqrMagnitude;
if (distance <= range)
{
float dot = Vector3.Dot(targetDir, dirVector);
if (dot * dot >= cos * distance)
{
enemies.Add(enemy);
}
}
}
}
return enemies;
}
코드 부연설명
정규화는 성능에 좋지 못하기에 게임에서 성능을 최적화하기 위해
(cosθ')^2 <= (A·B)^2 / |A|^2 * |B|^2와 같이 제곱하여 계산하였고,
그 중, A 벡터의 크기는 여러 번 재사용 가능하기에 매 번 곱해주는 대신 정규화하여 변수에 넣어주었다.
(cosθ')^2 <= (A·B)^2 / |B|^2가 되었고, 나누기보다는 곱셈을 사용하는 것이 더 좋기에
(cosθ')^2 * |B|^2 <= (A·B)^2로 계산해주었다.
※ |B|^2 = sqrMagnitude를 사용하여 구할 수 있다.
2. 직선 범위 내에 적이 존재하는지 판단하기

적이 직선 범위(빨간 직사각형) 내에 존재하는지 파악하기 위해
우리가 구해야 할 것은
1. N이 정면 범위 내에 있는가?
2. M이 측면 범위 내에 있는가?
이 두 가지를 확인하면 된다.
각각 벡터의 내적과 외적을 사용하여
N과 M의 길이를 구할 수 있다.
1. N이 정면 범위 내에 있는가?
N의 길이를 구하기 위해서는 기본적으로 삼각함수의 성질을 사용할 수 있다.
위 그림을 90˚ 회전시켜보면 다음과 같은 그림이 된다.
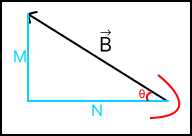
삼각함수의 성질을 적용하면 우리가 구해야할 N은 |B|cosθ 임을 알 수 있다.
근데 이 식을 보면 벡터의 내적 공식과 닮아 있다.
A·B = |A||B|cosθ이 식에서 N과 방향이 일치하는 A벡터를 정규화하면
A·B = |B|cosθ우리가 구해야할 N의 길이가 되는 것을 볼 수 있다.
N이 정면 범위 내에 존재한다면 적이 있는 것이고, 존재하지 않는다면 적이 없는 것이다.
2. M이 측면 범위 내에 있는가?
M의 길이를 구하기 위해서는 벡터의 외적의 성질을 알아야한다.

외적의 크기는 평행사변형의 넓이와 같은데, 이를 식으로 풀이해보면
|A×B| = |A|× M (M=|B|sinθ)이 된다.
우리는 M을 구해야하기에 위 식을
M = |A×B| / |A|로 정리할 수 있다.
위 식을 계산하면 |A||B|sinθ / |A| 으로 A벡터의 길이가 약분되기 때문에
계산의 편의성을 위해서 A벡터를 정규화하면
M = |A×B|로 M의 길이는 벡터의 외적이 된다.
M이 측면 범위 내에 존재한다면 적이 있는 것이고, 존재하지 않는다면 적이 없는 것이다.
두 가지 경우를 모두 비교한다면 특정 방향으로 직사각형 내에 적이 존재하는지를 판별할 수 있는 코드를 구현할 수 있다.
다음은 적용한 코드이다.
private List<EnemyUnit> GetAllEnemiesInStraight(Vector3 unitPos, Vector3 targetDir, float range, float width)
{
List<EnemyUnit> enemies = new List<EnemyUnit>();
targetDir = targetDir.normalized;
float widthThreshold = (width * 0.5f) * (width * 0.5f);
foreach (EnemyUnit enemy in _enemies)
{
if (enemy != null && enemy.isActiveAndEnabled)
{
Vector3 dirVector = enemy.transform.position - unitPos;
// 유닛을 기준으로한 정면 거리
float forwardDist = Vector3.Dot(targetDir, dirVector);
if (forwardDist < 0 || forwardDist > range) continue;
// 유닛을 기준으로한 측면 거리
float sideDist = Vector3.Cross(targetDir, dirVector).sqrMagnitude;
if (sideDist <= widthThreshold)
{
enemies.Add(enemy);
}
}
}
return enemies;
}'공부 > 유니티' 카테고리의 다른 글
| [Unity] 툴팁 만들기 - part2. 런타임 중에 툴팁에 데이터 넣기 (0) | 2025.05.22 |
|---|---|
| [Unity] 툴팁 만들기 - part1. 배치된 툴팁 (0) | 2025.05.21 |
| [Unity] Custom Editor - ReorderableList (0) | 2024.06.11 |
| [Unity] 유니티 어트리뷰트 만들기 (0) | 2024.02.24 |
| [Unity] 유니티 어트리뷰트 모음 (0) | 2024.02.24 |





